Ein Anfänger-Tutorial zum Erlernen der Confusion Matrix im maschinellen Lernen.
Dieses Jahr war ein Jahr der Innovationen im Bereich der Datenwissenschaft, wobei künstliche Intelligenz und maschinelles Lernen die Schlagzeilen beherrschten. Obwohl es keinen Zweifel an den Fortschritten im Jahr 2023 gibt, ist es wichtig zu erkennen, dass viele dieser Fortschritte im Bereich des maschinellen Lernens nur aufgrund der richtigen Bewertungsprozesse möglich waren, denen die Modelle unterzogen werden. Datenpraktiker haben die Aufgabe, sicherzustellen, dass genaue Bewertungen und Prozesse durchgeführt werden, um die Leistung eines Modells für maschinelles Lernen zu messen. Dies ist nicht nur von Vorteil, sondern unerlässlich.
Wenn Sie die Kunst der Datenwissenschaft erlernen möchten, führt Sie dieser Artikel durch die entscheidenden Schritte der Modellbewertung mithilfe der confusion matrix, einem relativ einfachen, aber leistungsstarken Tool, das bei der Modellbewertung weit verbreitet ist.
Tauchen wir also ein und erfahren Sie mehr über die confusion matrix.
Was ist die Verwirrungsmatrix?
Die confusion matrix ist ein Tool zur Bewertung der Leistung eines Modells und wird visuell als Tabelle dargestellt. Sie bietet Datenexperten tiefere Einblicke in die Leistung, Fehler und Schwächen des Modells. Auf diese Weise können Datenexperten ihr Modell durch Feinabstimmung weiter analysieren.
Die Struktur der Verwirrungsmatrix
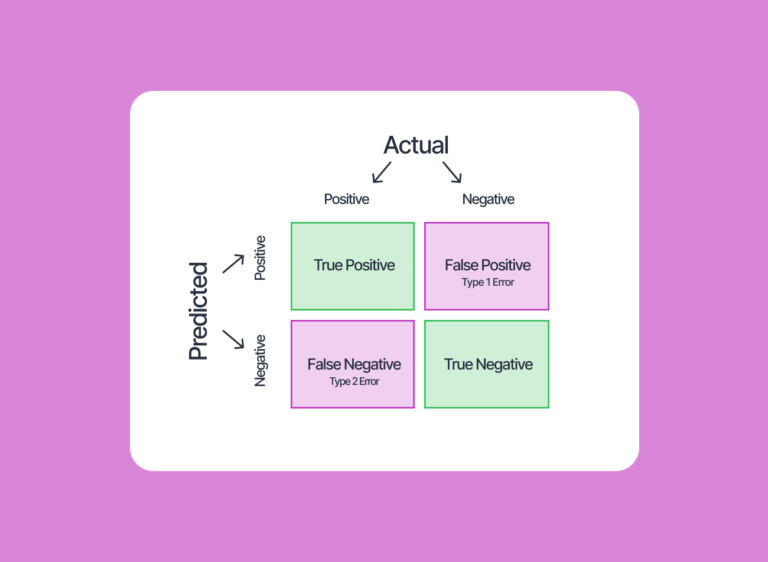
Lernen wir die Grundstruktur einer confusion matrix am Beispiel der Identifizierung einer E-Mail als Spam oder Nicht-Spam kennen.
- True Positive (TP) – Ihr Modell hat die positive Klasse vorhergesagt. Beispielsweise die Identifizierung einer Spam-E-Mail als Spam.
- True Negative (TN) – Ihr Modell hat die negative Klasse korrekt vorhergesagt. Beispielsweise wird eine normale E-Mail nicht als Spam identifiziert.
- Falsch-positiv (FP) – Ihr Modell hat die positive Klasse falsch vorhergesagt. Beispielsweise wurde eine normale E-Mail als Spam identifiziert.
- Falsch-Negativ (FN) – Ihr Modell hat die negative Klasse falsch vorhergesagt. Beispielsweise wurde eine Spam-E-Mail als normale E-Mail identifiziert.
Um das Konzept einer confusion matrix wirklich zu verstehen, werfen Sie einen Blick auf die folgende Visualisierung:
Terminologie der Verwirrungsmatrix
Um die Confusion Matrix gründlich zu verstehen, ist es wichtig, die wichtigen Kennzahlen zu kennen, die zur Messung der Leistung eines Modells verwendet werden.
Lassen Sie uns wichtige Kennzahlen definieren:
Genauigkeit – hier wird die Gesamtzahl der korrekten Klassifizierungen geteilt durch die Gesamtzahl der Fälle gemessen.
Die Rolle einer Verwirrungsmatrix
Um die confusion matrix besser zu verstehen, müssen Sie ihr Ziel und den Grund ihrer weiten Verbreitung verstehen.
Wenn es darum geht, die Leistung eines Modells oder etwas ganz anderes zu messen, konzentrieren sich die Leute auf Genauigkeit. Sich jedoch stark auf die Genauigkeitsmetrik zu verlassen, kann zu falschen Entscheidungen führen. Um dies zu verstehen, werden wir die Einschränkungen durchgehen, die die Verwendung von Genauigkeit als eigenständige Metrik mit sich bringt.
Einschränkungen der Genauigkeit als eigenständige Metrik
Wie oben definiert, misst die Genauigkeit die Gesamtzahl der korrekten Klassifizierungen geteilt durch die Gesamtzahl der Fälle. Die Verwendung dieser Metrik als eigenständiges Maß ist jedoch mit Einschränkungen verbunden, beispielsweise:
- Arbeiten mit unausgewogenen Daten : Keine Daten sind perfekt und die Verwendung der Genauigkeitsmetrik sollte anhand ihrer Vorhersagekraft bewertet werden. Wenn Sie beispielsweise mit einem Datensatz arbeiten, in dem eine Klasse eine andere überwiegt, erreicht das Modell eine höhere Genauigkeitsrate, da es die Mehrheitsklasse vorhersagt.
- Fehlertypen : Wenn Sie die Leistung Ihres Modells in einem bestimmten Kontext verstehen und kennenlernen, können Sie seine Leistung optimieren und verbessern. Wenn Sie beispielsweise mithilfe einer confusion matrix zwischen den Fehlertypen unterscheiden, z. B. FP und FN, können Sie die Einschränkungen des Modells ermitteln.
Aufgrund dieser Einschränkungen bietet die confusion matrix zusammen mit der Vielzahl an Metriken detailliertere Einblicke, wie die Leistung eines Modells verbessert werden kann.
Die Vorteile einer confusion matrix
Wie in der Grundstruktur einer confusion matrix zu sehen ist, werden die Vorhersagen in vier Kategorien unterteilt: Richtig positiv, Richtig negativ, Falsch positiv und Falsch negativ.
Diese detaillierte Aufschlüsselung bietet wertvolle Erkenntnisse und Lösungen zur Verbesserung der Leistung eines Modells:
- Unausgewogene Daten lösen : Wie bereits erwähnt, ist die Verwendung von Genauigkeit als eigenständige Metrik bei unausgewogenen Daten mit Einschränkungen verbunden. Die Verwendung anderer Metriken wie Präzision und Rückruf ermöglicht eine ausgewogenere Ansicht und genauere Darstellung. Beispielsweise können falsch positive und falsch negative Ergebnisse in Sektoren wie dem Finanzwesen schwerwiegende Folgen haben.
- Differenzierung nach Fehlertypen : Durch das Verständnis der unterschiedlichen Fehlertypen, die das maschinelle Lernmodell erzeugt, erfahren Sie mehr über dessen Grenzen und Verbesserungsbereiche.
- Kompromisse : Der Kompromiss zwischen der Verwendung verschiedener Metriken in einer confusion matrix ist wichtig, da sie sich gegenseitig beeinflussen. Beispielsweise führt eine Erhöhung der Präzision normalerweise zu einer Verringerung der Rückrufquote. Dies hilft Ihnen dabei, die Leistung des Modells mithilfe von Wissen aus den betroffenen Metrikwerten zu verbessern.
Berechnen einer confusion matrix
Nachdem wir nun ein gutes Verständnis einer grundlegenden confusion matrix, ihrer Terminologie und ihrer Verwendung haben, fahren wir mit der manuellen Berechnung einer confusion matrix fort, gefolgt von einem praktischen Beispiel.
Manuelles Berechnen einer confusion matrix
Hier finden Sie eine Schritt-für-Schritt-Anleitung zum manuellen Berechnen einer confusion matrix.
- Definieren Sie die Ergebnisse
Der erste Schritt besteht darin, die beiden möglichen Ergebnisse Ihrer Aufgabe zu identifizieren: Positiv oder Negativ.
- Sammeln der Vorhersagen
Sobald Ihre möglichen Ergebnisse definiert sind, besteht der nächste Schritt darin, alle Vorhersagen des Modells zu sammeln, einschließlich der Häufigkeit, mit der das Modell jede Klasse und ihr Vorkommen vorhergesagt hat.
- Klassifizierung der Ergebnisse
Nachdem alle Vorhersagen gesammelt wurden, besteht der nächste Schritt darin, die Ergebnisse in die folgenden vier Kategorien einzuteilen:
- Wahres Positiv (TP)
- Wahres Negativ (TN)
- Falsch-Positiv (FP)
- Falsch-Negativ (FN)
- Erstellen einer Matrix
Nachdem die Ergebnisse klassifiziert wurden, besteht der nächste Schritt darin, sie in einer Matrixtabelle darzustellen, um sie anhand verschiedener Kennzahlen weiter zu analysieren.
confusion matrix – Praktisches Beispiel
Lassen Sie uns diesen Vorgang anhand eines praktischen Beispiels demonstrieren.
Bleiben wir beim Beispiel der Identifizierung einer E-Mail als Spam oder Nicht-Spam und erstellen wir einen hypothetischen Datensatz, bei dem Spam positiv und Nicht-Spam negativ ist. Wir haben die folgenden Daten:
- Unter den 200 E-Mails befinden sich 80 E-Mails, bei denen es sich tatsächlich um Spam handelt. 60 davon werden vom Modell korrekt als Spam (TP) identifiziert .
- Unter den 200 E-Mails sind 120 E-Mails kein Spam, von denen das Modell 100 korrekt als Kein Spam (TN) identifiziert.
- Unter den 200 E-Mails identifiziert das Modell 20 E-Mails, die kein Spam sind , fälschlicherweise als Spam (FP).
- Unter den 200 E-Mails übersieht das Modell 20 Spam-E-Mails und identifiziert sie als Kein-Spam (FN).
An diesem Punkt haben wir das Ergebnis definiert und die Daten gesammelt. Der nächste Schritt besteht darin, die Ergebnisse in die vier Kategorien zu klassifizieren:
- Richtig positiv: 60
- Wahres Negativ: 100
- Falsch-Positiv: 20
- Falsch-Negativ: 20
Der nächste Schritt besteht darin, daraus eine confusion matrix zu machen:
| Tatsächlich / Vorausgesagt | Spam (positiv) | Kein Spam (Negativ) |
| Spam (positiv) | 60 (ZP) | 20 (FN) |
| Kein Spam (Negativ) | 20 (Vorderansicht) | 100 (TN) |
Was also sagt uns die Verwirrungsmatrix?
- Die wahren Positiven und wahren Negativen weisen auf genaue Vorhersagen hin.
- Die falsch-positiven Ergebnisse zeigen an, dass das Modell die positive Klasse falsch vorhergesagt hat.
- Die falsch-negativen Ergebnisse zeigen an, dass das Modell die positive Klasse nicht identifizieren und vorhersagen konnte.
Mithilfe dieser confusion matrix können wir die verschiedenen Metriken berechnen: Genauigkeit, Rückruf/Empfindlichkeit, Präzision, Spezifität und den F1-Score.
Präzision vs. Rückruf
Sie fragen sich vielleicht, warum der F1-Score Präzision und Rückruf in seiner Formel berücksichtigt. Die Metrik des F1-Scores ist entscheidend, wenn Sie mit unausgewogenen Daten arbeiten oder wenn Sie den Kompromiss zwischen Präzision und Rückruf ausbalancieren möchten .
Die Präzision misst die Genauigkeit einer positiven Vorhersage. Sie beantwortet die Frage: „Wie oft lag das Modell richtig, wenn es WAHR vorhergesagt hat?“. Die Präzision ist insbesondere dann wichtig, wenn die Kosten eines falsch positiven Ergebnisses hoch sind.
Der Rückruf oder die Sensitivität misst die Anzahl der tatsächlich positiven Ergebnisse, die vom Modell richtig identifiziert wurden. Sie beantwortet die Frage: „Wenn die Klasse tatsächlich WAHR war, wie oft lag der Klassifikator richtig?“.
Das Erinnern ist wichtig, wenn sich das Übersehen einer positiven Instanz (FN) als wesentlich schlimmer erweist, als negative Instanzen fälschlicherweise als positiv zu kennzeichnen.
- Präzisionsverwendung : Falsche Positivmeldungen können schwerwiegende Folgen haben. Beispielsweise hat ein im Finanzsektor verwendetes Klassifizierungsmodell eine Transaktion fälschlicherweise als betrügerisch eingestuft. In solchen Szenarien ist die Präzisionsmetrik wichtig.
- Verwendung von Rückrufen : Die Identifizierung aller positiven Fälle kann zwingend erforderlich sein. Beispielsweise kann es schädlich sein, wenn Klassifizierungsmodelle im medizinischen Bereich keine korrekte Diagnose stellen. In Szenarien, in denen die korrekte Identifizierung aller positiven Fälle unerlässlich ist, ist die Rückrufmetrik wichtig.
Verwirrungsmatrix mit Scikit-learn in Python
Um dies ins rechte Licht zu rücken, erstellen wir mit Scikit-learn in Python eine confusion matrix unter Verwendung eines Random-Forest-Klassifikators .
Der erste Schritt besteht darin, die erforderlichen Bibliotheken zu importieren und Ihren synthetischen Datensatz zu erstellen Stable Diffusion 2.
Der nächste Schritt besteht darin, das Modell mit einem einfachen Random-Forest-Klassifikator zu trainieren
Wie im praktischen Beispiel müssen wir die Ergebnisse klassifizieren und in eine confusion matrix umwandeln. Dazu erstellen wir zunächst Vorhersagen auf der Grundlage der Testdaten und generieren dann eine confusion matrix:
Nun wollen wir eine visuelle Darstellung der confusion matrix erzeugen:
Dies ist die Ausgabe:
Tada 
Fazit
In diesem Artikel haben wir die Definition einer confusion matrix, wichtige Begriffe rund um das Bewertungstool sowie die Einschränkungen und Bedeutung der verschiedenen Metriken untersucht. Die Fähigkeit, eine confusion matrix manuell zu berechnen, ist für Ihre datenwissenschaftliche Wissensbasis ebenso wichtig wie die Fähigkeit, sie mithilfe von Bibliotheken wie Scikit-learn auszuführen.
Wenn Sie tiefer in die Confusion Matrix eintauchen möchten, üben Sie Konfusionsmatrizen in R mit Understanding Confusion Matrix in R. Tauchen Sie mit unserem Kurs „Modellvalidierung in Python“ noch etwas tiefer ein , wo Sie die Grundlagen der Modellvalidierung und Validierungstechniken erlernen und mit der Erstellung validierter und leistungsstarker Modelle beginnen.